Аннотация. Рассматриваются два алгоритма автоматического управления объекта в трёхмерном пространстве: классический и нейросетевой. Приводятся сравнительные оценки их качественных показателей регулирования. Указываются
их преимущества и недостатки
Ключевые слова. Трехмерное пространство, автоматическое классическое, нейросетевое управление, качественные показатели регулирования.
Предисловие
При сборке космических станций на орбите возникает задача по сближению, причаливанию и состыкованию отдельных блоков. Данная задача реализуется ручным либо автоматическим режимами.
Рассмотрим задачу управления процессом стыковки в автоматическом режиме. Наиболее рациональное решение задачи получается,когда один объект является «активным», а другой –«пассивным». Активный объект осуществляет поиск и движение в пространстве к пассивному объекту по измеренным его координатам. Пассивный объект ориентирован в пространстве по системе координат X,Y,Z и служит целью для активного объекта.
Активный объект снабжён устройствами, обеспечивающими его движение по определённой траектории, соединяющей центр тяжести объекта с целью. Последняя может быть неподвижной или движующейся в пространстве по определённой траектории.
Для достижения цели объект имеет устройство, следящее за целью и непрерывно определяющее взаимное расположение объекта и цели путём измерения координат цели. Сведения,получаемые от измерительного устройства, используются для управления движением объекта. Центр тяжести объекта может занимать в пространстве различные положения, обусловленные его движением в неоднородной среде из-за неспокойного состояния окружающей среды, неточного управления и наличия различного рода помех.
Для эффективного управления движением объекта необходимо обеспечить устойчивость его движения. Решение этой задачи реализуется с привлечением различных дополнительных алгоритмов стабилизации активного объекта и в статье не рассматривается.
Постановка задачи
Исследуем автоматический принцип управления активным объектом в трёхмерном пространстве, реализуемый алгоритмами, использующими классический метод и искусственную нейронную сеть.
Цель движущего активного объекта –сближение с пассивным объектом цели, который может занимать в пространстве неподвижное положение или двигаться равномерно или ускоренно.
Задача- подучить сравнительные оценки текущей меры близости объекта к цели, если активный объект управляется с использованием двух различных алгоритмов регулирования.
Допущения
Структура математической модели объекта управления описывается линейным дифференциальным уравнением первого порядка .Параметры модели объекта неизвестны при нейросетевом подходе к решению задачи. Параметры нейрорегулятора обучаются и автоматически рассчитываются в реальном режиме в процессе управления объектом.
Разнообразные и сложные движения объекта в пространстве представим как сумму поступательного движения его центра тяжести, помещённого в начало прямоугольной системы координат Х,Y,Z, и вращательного движения относительно трёх перпендикулярных`осей X,Y,Z, имеющих определённую ориентацию в прстранстве. Ось Z направлена по касательной к траектории в сторону движения объекта. Будем считать, что ось Z совпадает с осью симметрии объекта и проведена перпендикулярно к плоскости осей X и Y.
Под действием возмущений объект может поварачиваться вокруг каждой из ориентированных осей X, Y, Z. Поворот корпуса объекта вокруг оси Z называют углом крена объекта. Угол между продольной осью объекта и поскостью движения, проходящей через точку старта и точку цели, называют углом рыскания. Угол между продольной осью объекта и плоскостью горизонта называют тангажём объекта. Способ определения этих углов основан на свойстве быстро вращающегося гироскопа и используется при стабилизации траектории движения активного объекта к цели. Активный объект содержит оборудование, позволяющее производить измерения координат пассивного объекта.
1. Классический подход к решению задачи
Трёхмерную систему регулирования в каждой плоскости будем представлять как связанную систему, в которй кроме основных каналов регулирования используются дополнительные статические устройства , призванные скомпенсировать перекрёстные связи, присущие многомерному объекту.
Применительно к рассматриваемому объекту, структурная схема связанного регулятора с нейтрализацией перекрёстных связей показана на рис.1.,где Dp1, Dp2 и Dp3- передаточные функции основных регуляторов, а Wk12, Wk21, Wk13, Wk31,Wk32, Wk23, - перекрёстные компенсирующие элементы и элементы объекта W11, W12, W13, W22, W21, W23, W33, W31, W32 .
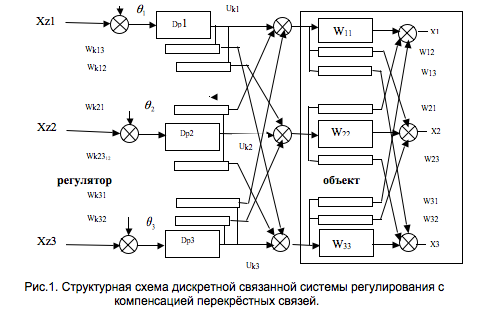
Рис.1. Структурная схема дискретной связанной системы регулирования компенсацией перекрёстных связей.
Из [1] следует, что условием развязки каналов регулирования по сигналам от заданных переменных Хz1 , Хz2 и Xz3 является диагональная матрица многосвязанной разомкнутой системы, т.е.
W Dp=D0 , (1)
где D0- обозначена диагональная матрица соответствующего размера.
Тогда передаточные функции Dp и W выразим в виде
C учётом (4-10), после несложных преобразований, получим для первого канала выражение зависимости выхода объекта от управляющего воздействия
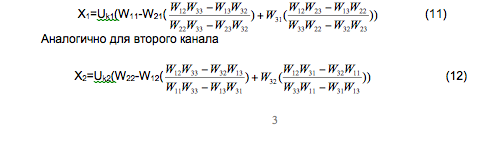
Для третьего канала
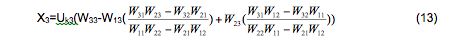
где Uk1 , Uk2 и Uk3 соответственно управляющие воздействия по первому , второму и третьему каналам регулирования.
Из выражений (11)- (13) следует, что в результате введения в многоконтурную систему компенсирующих элементов, выходные сигналы по каждому из каналов зависят только от управляющих воздействий по соответствующим каналам. Это означает,что задача синтеза основных регуляторов Dp1, Dp2 и Dp3 с многоконтурной структурой может быть сведена к их синтезу с одноконтурными структурами регулирования.
В этом случае из (11)-(13) выводятся эквивалентные передаточные функции для основных регуляторов по каждому каналу соответственно
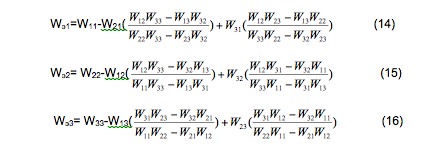
Таким образом, синтез основных регуляторов базируется на сведениях о параметрах модели объекта управления и о компонентах взаимных перекрёстных связей внутри объекта.
2. Синтез дискретных регуляторов управления движением объекта в трёхмерном пространстве
Рассмотрим управляемое устойчивое движение центра тяжести активного объекта в трёхмерном пространстве относительно двух плоскостей. Одна из них параллельна линии горизонта, а другая ей перпендикулярна.
Тогда передаточные функции объекта в обозначениях на рис.1. представим в виде.
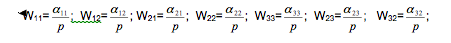
Из условий устойчивости объекта регулирования первого порядка необходимо, чтобы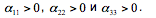 
Дискретную передаточную функцию эквивалентных объектов определим Z-преобразованием с использованием оператора преобразования Лапласа [2].
Для первого канала получим
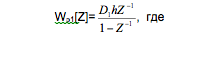
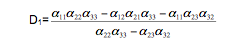
Соответственно для второго канала
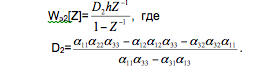
Наконец, для третьего канала имеем
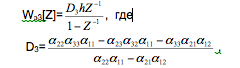
где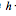 
- период дискретизации во времени.
Применяя Z-преобразование к управляющему воздействию на входе фиксатора нулевого порядка M[Z] и учитывая дискретную передаточную функцию участка «фиксатор нулевого порядка плюс объект регулирования» получим Z-изображение выхода системы по каждому каналу .Если нули полинома M[Z]
совпадают с полюсами эквивалентной передаточной функции Wэi[Z], то переходной процесс на выходе системы заканчивается за k-шагов квантования
независимо от состояния объекта регулирования [3].
Полагая для всех каналов системы регулирования Mi[Z]=K0i (I=1,2,3) , в окончательном виде определим их значения
Управление движением объекта по заданным стабильным координатам цели
в трёхмерном пространстве иллюстрируется на рис.2.
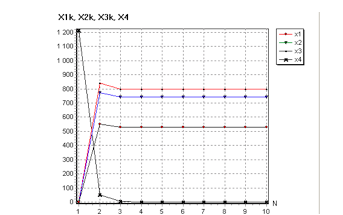
Рис.2. Зависимости процесса сближения объекта к цели по трём её координатам
X1, X2, X3 с оценкой их рассогласования X4 от количества шагов итерации.
При управлении сближением объекта к цели в одной горизонтальной плоскости состыкование осуществляется через три шага итерации без погрешности, но с перерегулированием.
Если положение цели в пространстве подвержено случайным и нестабильным воздействиям по трём координатам, то процесс сближения объекта к цели также становится нестабильным. На рис.3.система управления отслеживает нестабильность поведения цели, со среднеквадратической погрешностью 
<14 по всем координатам. При отсутствии случайной составляющей в поведении цели среднеквадратическое значение погрешности рассогласования не превосходит 
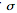<2.5.
Рис.3. Пошаговый процесс сближения управляемого объекта к цели в условиях
нестабильного поведения цели в пространстве.
3. Нейросетевой подход к решению задачи
Большинство работ по искусственным нейронным сетям, применяемых в системах управления динамическими объектами в трёхмерном пространстве, опубликованы в зарубежных изданиях. В частности, в [ 4,5] приведены методы синтеза нейросетевых автопилотов и систем управления угловым движением ракеты.
Условия, в которых совершается движение объекта, характеризуются неопределённостью и непредсказуюмостью. Будем считать, что известны координаты цели по высоте и на горизонтальной плоскости. Соответствующие координаты движущего объекта в любой момент времени определяются
системой управления путём отслеживания ошибки рассогласования между координатами объекта и соответствующими координатами цели. Допустим, что
при движении объекта в неоднородной среде сруктура его модели и её пораметры
изменяются и не отслеживаются. Это означает, что оптимальные параметры регулятора системы управления по классической схеме управления не могут быть предварительно рассчитаны.
Отказ от полного описания объектов определил переход к адаптивным системам регулирования,способным приспосабливаться к меняющимся в довольно широких пределах условиям функционирования объекта.
Элементарной базой, ориентированной на поддержку адаптивной технологии, может служить нейросетевая структура управления. На рис.4.
приведена структурная схема нейроуправления, содержащая три нейрона (N1,N2 и N3) с синаптическими весами wi0, wi1 и wi2 (i=1,2,3). Настройка весов производится методом обратного распространения ошибки рассогласования между координатами объекта и цели в реальном режиме в процессе управления движущимся объектом (символ z -1 рис.4. означает задержку сигнала на один такт, значения Xzi-обозначают заданные координаты цели, uki-управляющие воздействия на объект) [6,7].
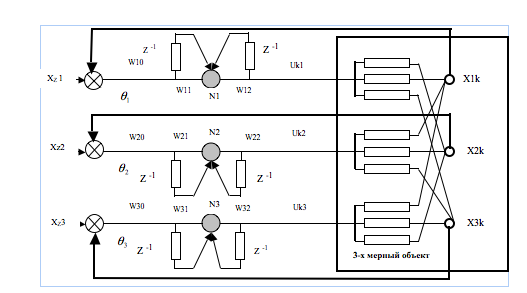
Рис.4. Структурная схема нейроуправления трёхмерного объекта
Синаптические веса нейронов на рис.4 по первому каналу выразим следующим образом:
Сравнивая структуры выражений (12) и (11), можно отметить, что нейросетевой подход к решению задачи автоматически реализует условие развязки многоконтурных каналов регулирования на одноконтурные структуры .
4.Исследование точности сближения объекта к неподвижной цели при параметрах, лежащих в одной плоскости с углом тангажа равным нулю.
1. На рис.5.иллюстрируется характер изменения координат активного объекта X1k,X2k и X3k в процессе пошагового нейроуправления его движением.Зависимость x4 отражает изменение расстояния объекта до цели в условиях,когда цель неподвижна,а объект не подвержен влиянию окружающей среды. Из трёх координат пассивного объекта только одна заданная координата отлична от нуля и определяет размер расстояния между активном объектом и целью по линии визирования, лежащей в одной плоскости,соединяющей объект и цель. Иными словами, активный и пассивный объекты находятся на одной плоскости с расстоянии между ними Х4.
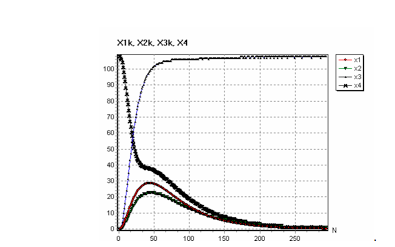
Рис.5. Изменения координат объекта и меры сближения Х4 объекта к неподвижной цели в горизонтальной плоскости
Из рис.5. следует, что момент стыковки реализуется на 250 шаге итерации, и при этом объект по координатам X1k и X2k на 45-м шаге имеет наибольшее отклонение в горизонтальной плоскости, проходящей между объектом и целью. Отклонение обусловлено тем, что автоматически изменяются параметры регулятора .Это приводит к относительной погрешности изменения положения объекта по координатам Х1к и Х2к, выраженных в процентах на рис.6 в зависимости от шагов итерации N .
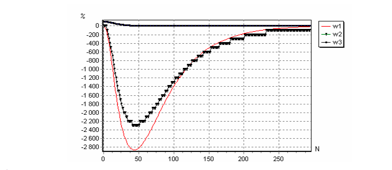
Рис.6. Зависимость относительной погрешности координат сближения объекта к цели в горизонтальной плоскости от количества итераций
Из анализа рис.5. и рис.6. следует, что отклонения активного объекта от горизонтальной плоскости выполняется только по тем координатам, значения которых в начале равны координата цели. При этом глубина отклонения зависит от величины расстояния между объектом и целью. С увеличением этой глубина отклонения только увеличивается.
Таким образом, если объект и цель располагаются достаточно близко и по своим параметрам принадлежат к одной горизонтальной плоскости, то захвата и фиксации пассивного объектами может произойти только на 250 шаге итерации . С увеличением расстояния между объектом и целью момент захвата и фиксации может быть выполнен уже на меньшем шаге итерации.
Если все заданные координаты цели соизмеримы между собой и угол тангажа отличен от нуля, то изменения координат объекта в пространстве приобретают иную зависимость.
5.Исследование движения объекта в трёхмерном пространстве
На рис.7.приведены зависимости изменений координат объекта в обозначениях: кривая x1-соответствует значению на рис.4. координате x1k, кривая x2-значению x2k, кривая x3-значению x3k. Зависимость вида х4-определяет изменение расстояния объекта до цели в условиях,когда цель неподвижна,а объект не подвержен влиянию окружающей среды. Угол тангажа при этом отличен от нуля.
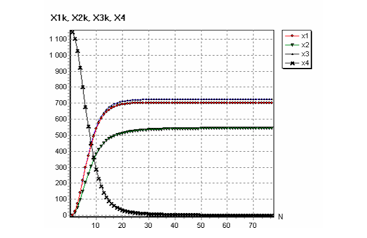
Рис.7.Изменения координат объекта и мера сближения объекта к неподвижной цели с углом тангажа, отличным от нуля, в зависимости от шага итерации.
Относительная погрешность в процентах от шага итерации при сближении координат объекта к заданным значениям цели иллюстрируется на рис.8.
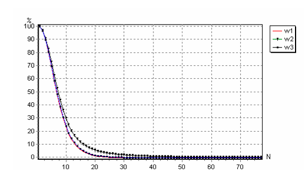
Рис.8. Зависимость изменения относительной погрешности сближения объекта к цели при различных шагах итерации.
Из анализа приведенных рисунков 7 и 8 следует, что в идеальном варианте объект достигает цель спустя пятьдесят шагов итерации. С уменьшением высоты цели число шагов итерации обычно увеличивается. С увеличеним высоты количество шагов итерации уменьшается. Это явление обусловлено свойством нейроуправления:чем больше расстояние между объектом и целью,тем больше образуется размер управляющего воздействия на объект.
6.Исследование движения объекта к неподвижной цели в неоднородной среде.
Пусть объект в процессе движения подвержен вращению вокруг пространственных координат X,Y и Z от случайных факторов с равномерным законом распределения. На рис.9.приводится характер поведения координат объекта в процессе движения активного объекта к цели, находящейся неподвижно на высоте 700 условных единиц.
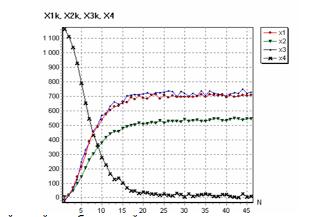
Рис.9. Устойчивый колебательный процесс управляемых координат объекта при движении его к неподвижной цели в условиях неоднородной среды.
На всём интервале шагов движения объект сближается к цели, совершая при этом колебания вокруг неё. При этом переходной процесс на выходе объекта отсутствует. Зависимость относительной погрешности сближения объекта к цели с увеличением шагов итерации в неоднородной среде пространства представлена на рис.10.
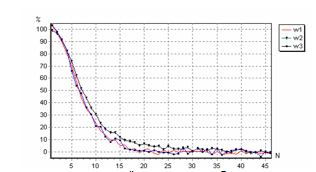
Рис.10 .Изменения относительной погрешности сближения координат объекта к цели в неоднородной среде пространства.
7.Исследование движения объекта к движущей цели в неоднородной среде
Объект вначале приближается к неподвижной цели, достигает её на двадцатом шаге итерации, а затем цель начинает двигаться от объекта с ускорением. На рис.11.иллюстрируется поведение данного объекта в этой ситуации.
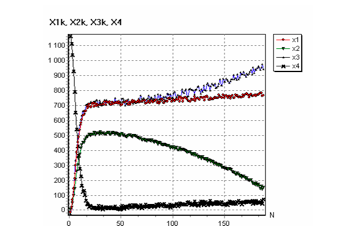Рис.11.Устойчивый колебательный процесс поведения объекта в уловиях неоднородной среды трёхмерного пространства.
Из рис.11. по характеру поведения кривой х4 следует,что объект начинает отставать от цели на пятидесятом шаге итерации.
Результат моделирования процесса движения объекта к цели,высота которой не остаётся постоянной, а имеет тенденцию к увеличению с ускорением, показывает, что относительная погрешность рассогласования координат объекта и цели с течением времени увеличивается.Это нетрудно заметиь на рис.12.
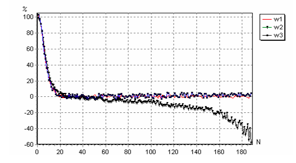
Рис.12. Изменения относительной погрешности рассогласования между объектом и целью при непрерывном росте высоты цели, движущейся относительно активного объекта с ускорением.
По данным рис.11. нетрудно заметить, что при суммарном воздействии вращательных движений на объект относительно трёх перпендикулярных осей в пространстве их состояний техническая устойчивость нейроуправления обеспечивается на всёх шагах управления.
Анализируя материал исследований следует отметить,что алгоритм управления позволяет варьировать временем сближения объекта к цели, путём подбора соответствующих параметров , ограничивающих размер ошибки рассогласования между координатами объекта и цели.
8.Точностные показатели двух подходов в реализации алгоритма автоматического управления по сближению объекта к движущейся цели, подверженной случайным воздействиям
В таблицах приведены значения среднеквадратических погрешностей рассогласований между параметрами объекта и движущейся цели без учёта погрешностей, образованной в период времени обучения нейрорегулятора.
Таким образом, классический подход при реализации алгоритма управления движущимся объектом в сравнении с нейросетевым подходом обладает меньшей погрешностью. Эта тенденция наблюдается для классического подхода и при отсутствии случайных воздействий на тот же объект. В целом различия в погрешностях зависят главным образом от скорости обучения весовых коэффициентов нейронов и специфики нейрорегулятора как нестационарной системы, в которой процессы описываются дифференциальным уравнением с переменными в любой момент времени коэффициентами
В практическом плане качество процессов регулирования зависит от выбора алгоритма управления в связи с динамическими характеристиками объекта управления.
Выводы
1.Классический алгоритм управления превосходит нейросетевой по меньшей величине времени регулирования и уступает по минимальной площади переходного процесса.
2.Расчёт оптимальных параметров регулятора в классической схеме зависит от известных параметров объекта.
3.Моменты сближения, причаливания и состыкования активного объета к пассивному объекту при нейроуправлении зависят от соразмерности их координат.
4.Подбор размера ошибок рассогласования по координатам движущегося объекта и его цели в алгоритме нейрорегулирования влияет на время сближения объекта к цели .
5.Нейросетевой принцип управления обеспечивает устойчивое поведение объекта в пространстве при отказе от полного его математического описания за счёт приспособления управляющей системы к свойсвам конкретного объекта.
6.Нейросетевая система автоматического управления в ходе управления движущимся объектом всегда достигает за конечное время заданную цель или приближается к ней с некоторым отставанием во времени.
7.Нейросетевой подход к связанному управлению, в отличие от классического, автоматизирует процесс разделения многоконтурной структуры на одноконтурные.
Литература
1.Изерман Р.Цифровые системы управления.М.:Мир,1984,с.542.
2.Сигалов Г.Г., Мадорский Л.С. Основы теории дискретных систем управления. Минск, Высшая школа,1973,334с.
3.Гостев В.И. Системы управления с цифровыми регуляторами Справочник. К.:Техника,1990,280с.
4.Suykens Johan A. K.,Vandewalle Joos P. L.,De Moor Bart L. R., Artificial
Neural Networks for Modelling and Conrtol of Non-Linear Systems. Kluwer Academic Publishers. Boston / Dordrecht / London. 1997,235 p.
5.McFarLand M. B., Calise A. J.. Multylayer Neural Netwotks and Adaptive
Nonlinear Control of Angle Anti-Missiles.// AIAA Guidance, Navigation and Control Conference, August, 1997.
6.Макаров Г.Н. НЕЙРОУПРАВЛЕНИЕ ДВУМЕРНОГО ДИНАМИЧЕСКОГО ОБЪЕКТА.-Нейрокомпьютеры: разработка, применение, №10, 2009.
7.Горбань А.Н. Обучение нейронных сетей.- М.: СП «ParaGraph»,1990-160 с.
RESEARCH OF CONTROLLED MOVEMENT OF OBJECT
IN NON-UNIFORM THREE-DIMENSIONAL SPACE
G.N.Makarov
Smolensk, Russia e-mail:makarov1116@mail.ru
The summary. Two algorithms of automatic control of object in three-dimensional space are considered{examined}: classical and Neural Networks. Comparative ratings of their quality indicators of regulation are resulted. Are specified
Their advantages and lacks
Keywords. Space, automatic classical, Neural Networks management, quality indicators of regulation.
